탐색 알고리즘

이번에 알아볼 알고리즘은 가장 기본적인 선형 자료구조 탐색 알고리즘이다. 

 

선형 탐색 알고리즘은 전제 조건으로 자료가 정렬되어있어야 한다. 

정렬 알고리즘은 다음에 이어서 포스팅 하도록 하겠습니다 너무 많...

 

1. 완전 탐색

 

가장 간단하게 모든 원소를 탐색하는 방법

 

public static void main(String[] args) {
        int[] intArray = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        int targetNum = 6;
        for(int idx = 0; idx < intArray.length; idx++) {
            if(targetNum == intArray[idx]) {
                System.out.println("Target Number Index : " + idx);
                break;
            }
        }
    }

 

입력 크기가 n 일 때 찾으려는 대상이 앞에 있다면 시간이 짧겠지만 가장 큰 원소일 경우에는 n 번 걸리게 되므로 완전 탐색의 시간 복잡도는 O(n) 이다.

 

 

2. 이진 탐색

 

중간 인덱스의 원소와 찾으려는 대상의 대소를 비교하며 탐색하는 방법

 

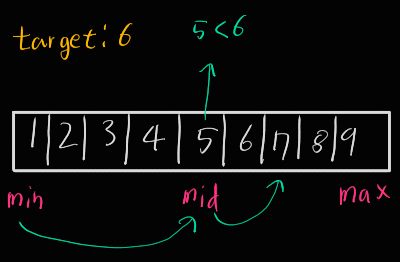
최소, 중간, 최대 인덱스를 위와 같이 찾으려는 대상과 인덱스의 값과 비교해가며

만약 중간 값보다 크다면 중간 값 이하로는 검사할 필요가 없으니 최소 값을 중간 값으로 

중간 값을 최신화 된 최소 값과 최대 값을 통해 갱신한 뒤 이 과정을 반복하여 

결과적으로 중간 값과 찾는 대상이 같을 경우 인덱스가 찾으려는 대상의 위치인 것을 알 수 있다. 

 

public static void main(String[] args) {
        int[] intArray = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        int targetNum = 6;
        int minIdx = 0;
        int maxIdx = intArray.length-1;
        int midIdx = (minIdx + maxIdx)/2;
        while(intArray[midIdx] != targetNum) {
            if(targetNum < intArray[midIdx]){
                maxIdx = midIdx;
                midIdx = (minIdx + maxIdx)/2;
            }else{
                minIdx = midIdx;
                midIdx = (minIdx + maxIdx)/2;
            }
        }
        System.out.println("Target Number Index: " + midIdx);
    }

 

이진 탐색은 완전 탐색의 상위호환이라고 봐도 무방할 정도로 시간복잡도가 O(logn) 으로 빠르다. 

 

다음에는 이어서 정렬 알고리즘에 대해 알아보고 구현해보도록 하자.