N-Queen

https://school.programmers.co.kr/learn/courses/30/lessons/12952

프로그래머스

 

Level 2

 

전공 교과 과정인 알고리즘에서 자주 다루는 문제인 N-Queen, 백트래킹을 활용해 여왕 배치 경우의 수를 구해야한다.

 

개념은 간단하다 체스의 여왕을 n x n 행렬(체스판)에 그 어떤 여왕도 잡히지 않는 n 개의 여왕 배치 방법을 구하는 것이다.

(체스에서 여왕은 상하좌우 직선 상 위치 그리고 양쪽 대각선 직선 상 위치에 모두 공격이 가능하다)

 

구현 방식은 r번째 행에 c번째 열에 여왕을 배치할 경우 

다음 r+1번째 행의 c(0~n) 열에 전부 배치가능한지 확인 후 불가능하다면 

r번째 행으로 돌아와 c+1번째 열에서 다시 진행하는 방식이다.

 

예시를 보자면

 

 

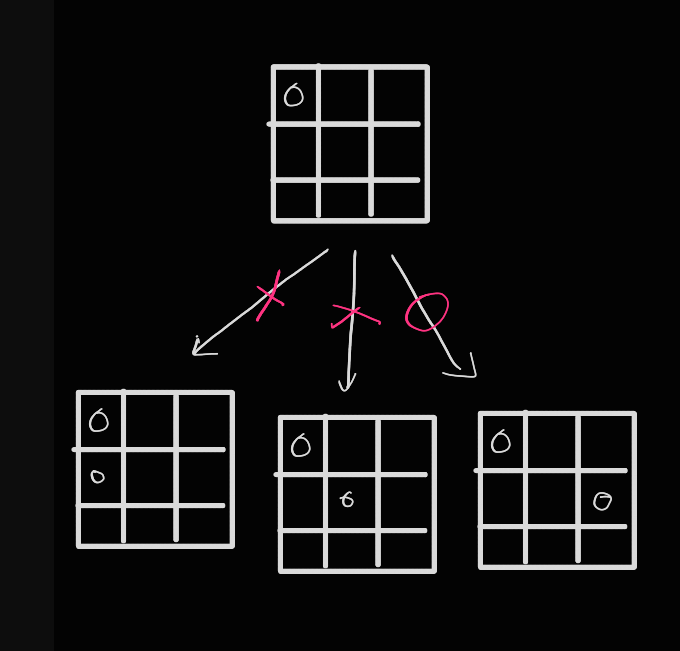
1,1에 배치할 경우 2행의 1열 2열은 진행이 불가능하다. 

이럴 경우 아래와 같이 다시 1행으로 넘어와 1,2에 배치한 뒤 다시 진행한다.

 

 

이 방법을 진행하면 결국 실패하는 경우는 미리 가지치기가 가능하고

결과적으로 최종 행에 도착하는 경우에만 배치 가능한 방법으로 판단할 수 있다. 

 

나의 경우에도 위의 방식을 거의 그대로 구현했으며

1행의 0~n 열부터 DFS 탐색을 진행하여 최종 행에 도달 시 결과값을 1 증가시킴으로 정답을 반환했다. 

단, 행렬이 1 X 1 일 경우에는 바로 1을 반환할 수 있게 했다. 

 

public class Solution { //N-Queen
    static int maxLen;
    static int answer;
    public int solution(int n) {
        maxLen = n;
        answer = 0;
        int[] queenColArr = new int[n]; //여왕들의 위치를 저장할 배열
        if(n == 1) return 1; //만약 행렬이 1x1 일 경우 1 반환 (Abnormal case)
        for(int col = 0; col < maxLen; col++) { //1행 0~n열 부터 진행
            queenColArr[0] = col; //1행 여왕 위치 저장
            dfs(1, queenColArr);
        }
        return answer;
    }

    public void dfs(int row, int[] colArr) {
        for(int col = 0; col < maxLen; col++) { //현재 행에서 0~n번째 열이 사용가능하지
            if(!isAttacked(row, col, colArr)) { //다른 여왕에게 공격당하는 위치가 아닐 경우
                if(row+1 == maxLen) { //다음 행이 없을 경우 종료
                    answer++;
                    return;
                }
                colArr[row] = col; //여왕 위치 저장
                dfs(row+1, colArr); //다음 행 진행
            }
        }
    }

    public boolean isAttacked(int row, int col, int[] colArr){
        for(int preRow = 0; preRow < row; preRow++) { //이전 여왕들의 위치 탐색
            int preCol = colArr[preRow];
            if(Math.abs(preCol-col) == (row-preRow) || preCol == col) //대각선, 동일 열 위치 확인
                return true; //공격당하는 것으로 판단
        }
        return false;
    }
}